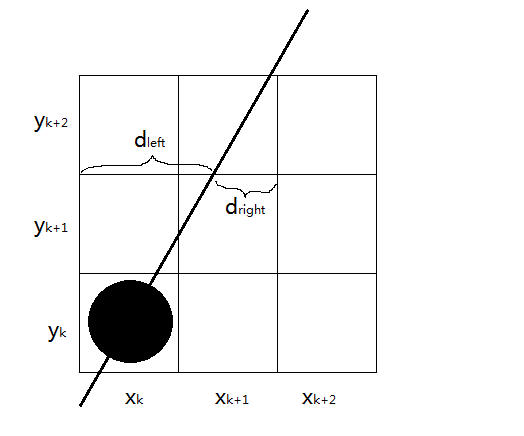場景中的直線由其兩端點的座標位置來定義。要在光柵監視器中顯示一條線段,圖形系統必須先將兩端點投影到整數屏幕座標,並確定離兩端點間的直線路徑最近的像素位置。接下來纔是將顏色填充到相應的像素座標。
前言
文章最後的演示代碼使用的是C++語言,函數庫使用的是以GLUT爲基礎的自定義封裝庫。本章內容將介紹生成直線的直線方程算法、DDA算法以及重要的Bresenham算法。
一、算法導論
以下僅僅展示算法的計算過程,具體實施請參考示例程序部分。
1.1直線方程算法
對於繪製直線來說,使用直線方程無疑是一種最直接的算法。在二維笛卡爾座標系中,直線方程爲:
y=m∗x+b(1.1)(1.1)y=m∗x+b
其中m代表直線的斜率,b爲直線的截距,對於任意兩個端點(x0,y0)(x0,y0)和(x1,y1)(x1,y1):
m=y1−y0x1−x0(1.2)(1.2)m=y1−y0x1−x0
b=y0−m∗x0(1.3)(1.3)b=y0−m∗x0
由於屏幕上的點在其座標系中以整數表示,當斜率 1>|m|1>|m| 時,我們可以以 xx 軸增量 δxδx 計算相應的y軸增量 δyδy:
δy=m∗δx(1.4)(1.4)δy=m∗δx
同樣,對於斜率 |m|>1|m|>1 的線段,我們需要通過以 yy 軸增量 δyδy 計算相應的 xx 軸增量 δxδx :
δx=δym(1.5)(1.5)δx=δym
通過使用直線方程繪製的點,其優點是算法簡單且精確,但是其在繪製每一個點的過程中都需要計算一次乘法和加法,顯而易見,由於乘法的存在,導致運算時間大幅度增加。接下來介紹的DDA算法將彌補直線方程的乘法缺陷。
1.2 DDA算法
從上可知,在繪製大量點的過程中,我們要儘可能的減少每一個點的計算時間。在計算機中加法運算是最簡單的運算之一了。我們可以利用直線的微分特性將每一步的乘法運算替換爲加法運算。數字微分分析法(Digital Differential Analyzer,DDA)是一種線段掃描轉換算法,基於式 (1.4)(1.4) 或 (1.5)(1.5) 來計算 δxδx 或 δyδy。
對於斜率 |m|≤1|m|≤1 的線段來說,我們仍以單位 xx (δx=1)(δx=1) 間隔(考慮到屏幕設備座標爲連續整數)取樣,並逐個計算每一個 yy 值。
yk+1=yk+m(1.6)(1.6)yk+1=yk+m
於是,我們便將乘法運算合理的轉換爲了加法運算。但是需要注意的是,在屏幕設備中的座標均是整數,所以我們在繪製時的y需要取整。
對於具有大於1的正斜率線段,則需要交換 xx 和 yy 的位置。也就是以單位 yy 間隔 (δy=1)(δy=1)取樣,順序計算每一個 xx 的值
xk+1=xk+1m(1.7)(1.7)xk+1=xk+1m
此時,每一個計算出的 xx 要沿着 yy 掃描線舍入到最近的像素位置。
該算法只需要計算出一個 stepstep 值( mm 或者 1m1m ),然後就可以沿着路徑的方向計算出下一位像素。然而,該算法的缺點顯而易見,在數學上,該算法能夠保證計算結果準確無誤,但是,由於計算機中的數據類型具有精度限制,這將會導致大量數據處理的誤差積累。並且,其雖然消除了直線方程中的乘法運算,但是對於浮點數的運算和取整仍然十分耗時。
1.3 Bresenham算法
接下來我們介紹由布萊森漢姆(Bresenham)提出的精確且高效的光柵線生成算法,該算法僅僅使用整數增量計算,除此之外,該算法還能應用於圓或者其他曲線。
我們將分別介紹四種斜率(m>1m>1 、 0<m<10<m<1 、 −1<m<0−1<m<0 和 m<−1m<−1)的計算過程(以下示例均爲從左至右畫線)。
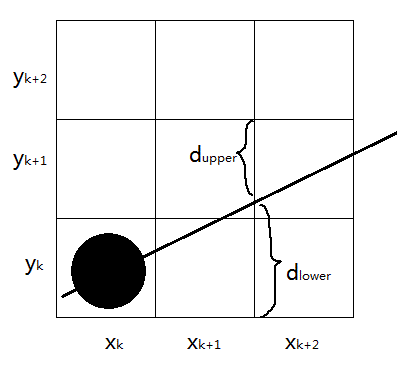
1.3.1 斜率大於1
![圖1.3.1_1]()
首先,在斜率大於1的情況下,沿路徑像素以單位 yy 間隔取樣。假設線段以(x0,y0)(x0,y0)開始對於其路徑上已繪製的(xk,yk)(xk,yk)點我們需要判定下一個點的繪製位置是(xk+1,yk+1)(xk+1,yk+1)還是(xk,yk+1)(xk,yk+1)。
在取樣位置 yk+1yk+1 我們使用 dleftdleft 和 drightdright 來標識兩個像素位置(xkxk與xk+1xk+1)與數學位置的水平偏移量。根據式 (1.1)(1.1) 可得在像素列 yk+1yk+1 處的 xx座標計算值爲
x=(yk+1−b)m=(yk+1−b)m(1.8)(1.8)x=(yk+1−b)m=(yk+1−b)m
所以
dleft=x−xk=yk+1−bm−xk(1.9)(1.9)dleft=x−xk=yk+1−bm−xk
且
dright=xk+1−x=xk+1−yk+1−bm(1.10)(1.10)dright=xk+1−x=xk+1−yk+1−bm
爲了確定兩個像素中哪一個更接近真實路徑,需要計算兩個像素偏移的差值。
dleft−dright=2yk+1−bm−2xk−1(1.11)(1.11)dleft−dright=2yk+1−bm−2xk−1
設線段終點位置爲(x1,y1)(x1,y1),可得
m=ΔyΔx=y1−y0x1−x0(1.12)(1.12)m=ΔyΔx=y1−y0x1−x0
設決策參數 pk=Δy(dleft−dright)pk=Δy(dleft−dright)
pk=2Δxyk−2Δyxk+C(1.13)(1.13)pk=2Δxyk−2Δyxk+C
其中
C=2Δx(1−b)−Δy(1.14)(1.14)C=2Δx(1−b)−Δy
在第 k+1k+1 步,決策參數可以由式(1.13)(1.13)計算得出
pk+1=2Δx(yk+1)−2Δyxk+1+C(1.15)(1.15)pk+1=2Δx(yk+1)−2Δyxk+1+C
將上述等式減去式(1.13)(1.13)可得決策值的增量δpk+1δpk+1
δpk+1=pk+1−pk=2Δx−2Δy(xk+1−xk)(1.16)(1.16)δpk+1=pk+1−pk=2Δx−2Δy(xk+1−xk)
其中xk+1−xkxk+1−xk的取值可能爲0,也可能爲1,這由前一個決策值pkpk的正負決定,也就是說如果pk<0pk<0,則下一個繪製的點是(xk,yk+1)(xk,yk+1) 否則繪製(xk+1,yk+1)(xk+1,yk+1)。並且繪製的點的位置又決定了該位置的決策值大小。
目前我們有了決策值之間的增量關係,僅需求出第一個決策值p0p0即可,由式(1.12)(1.12)、式(1.13)(1.13)、式(1.1)(1.1)和式(1.14)(1.14)聯立可得
p0=2Δx−Δy(1.17)(1.17)p0=2Δx−Δy
繪製過程解析:由於Δy>0Δy>0 所以當dleft>drightdleft>dright時(此時pk>0pk>0), 代表當前數學點更接近與xk+1xk+1否則更接近與xkxk。我們僅僅需要求出第一個決策值 p0p0 其後的決策值都是前一個決策值與決策增量δpk+1δpk+1的和。我們可以在沿線路徑的每一個 xkxk 處,進行下列檢測:
如果 pk<0pk<0 下一個要繪製的點是 (xk,yk+1)(xk,yk+1) ,並且 pk+1=pk+2Δypk+1=pk+2Δy
否則,下一個要繪製的點是 (xk+1,yk+1)(xk+1,yk+1) ,並且 pk+1=pk+2Δy−2Δxpk+1=pk+2Δy−2Δx
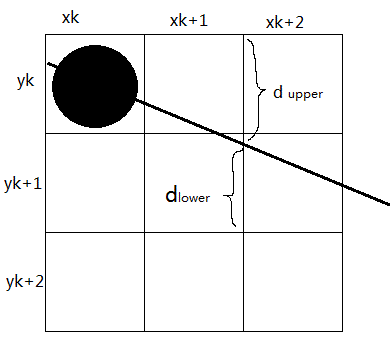
1.3.2 斜率大於0小於1
![圖1.3.2_1]()
在斜率大於0小於1的情況下,沿路徑像素以單位 xx 間隔取樣。假設線段以(x0,y0)(x0,y0)開始對於其路徑上已繪製的(xk,yk)(xk,yk)點我們需要判定下一個點的繪製位置是(xk+1,yk)(xk+1,yk)還是(xk+1,yk+1)(xk+1,yk+1)。
在取樣位置 xk+1xk+1 我們使用 dupperdupper 和 dlowerdlower 來標識兩個像素位置(ykyk與yk+1yk+1)與數學位置的水平偏移量。根據式 (1.1)(1.1) 可得在像素列 xk+1xk+1 處的 yy座標計算值爲
y=m(xk+1)+b(1.19)(1.19)y=m(xk+1)+b
所以
dlower=y−yk=m(xk+1)+b−yk(1.20)(1.20)dlower=y−yk=m(xk+1)+b−yk
且
dupper=yk+1−y=yk+1−m(xk+1)−b(1.21)(1.21)dupper=yk+1−y=yk+1−m(xk+1)−b
爲了確定兩個像素中哪一個更接近真實路徑,需要計算兩個像素偏移的差值。
dlower−dupper=2m(xk+1)−2yk+2b−1(1.22)(1.22)dlower−dupper=2m(xk+1)−2yk+2b−1
設決策參數 pk=Δx(dlower−dupper)pk=Δx(dlower−dupper)
pk=2Δyxk−2Δxyk+C(1.23)(1.23)pk=2Δyxk−2Δxyk+C
其中
C=2Δy+Δx(2b−1)(1.24)(1.24)C=2Δy+Δx(2b−1)
在第 k+1k+1 步,決策參數可以由式(1.23)(1.23)計算得出
pk+1=2Δy(xk+1)−2Δxyk+1+C(1.25)(1.25)pk+1=2Δy(xk+1)−2Δxyk+1+C
將上述等式減去式(1.23)(1.23)可得決策值的增量δpk+1δpk+1
δpk+1=pk+1−pk=2Δy−2Δx(yk+1−yk)(1.26)(1.26)δpk+1=pk+1−pk=2Δy−2Δx(yk+1−yk)
由式(1.12)(1.12)、式(1.23)(1.23)、式(1.1)(1.1)和式(1.24)(1.24)聯立可得第一個決策值p0p0
p0=2Δy−Δx(1.27)(1.27)p0=2Δy−Δx
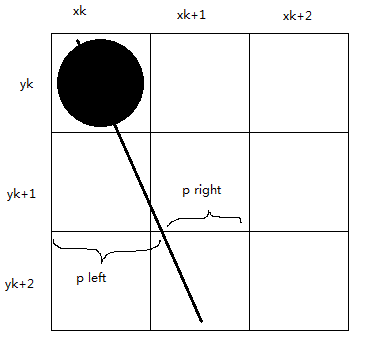
1.3.3 斜率大於-1小於0
![圖1.3.3_1]()
在斜率大於-1小於0的情況下,沿路徑像素以單位 xx 間隔取樣。假設線段以(x0,y0)(x0,y0)開始對於其路徑上已繪製的(xk,yk)(xk,yk)點我們需要判定下一個點的繪製位置是(xk+1,yk)(xk+1,yk)還是(xk+1,yk+1)(xk+1,yk+1)。
在取樣位置 xk+1xk+1 我們使用 dupperdupper 和 dlowerdlower 來標識兩個像素位置(ykyk與yk+1yk+1)與數學位置的水平偏移量。
dlower=y−yk+1=m(xk+1)+b−(yk−1)(1.28)(1.28)dlower=y−yk+1=m(xk+1)+b−(yk−1)
且
dupper=yk−y=yk−m(xk+1)−b(1.29)(1.29)dupper=yk−y=yk−m(xk+1)−b
爲了確定兩個像素中哪一個更接近真實路徑,需要計算兩個像素偏移的差值。
dupper−dlower=2yk−2m(xk+1)−2b−1(1.30)(1.30)dupper−dlower=2yk−2m(xk+1)−2b−1
設決策參數 pk=Δx(dupper−dlower)pk=Δx(dupper−dlower)
pk=2Δxyk−2Δyxk+C(1.31)(1.31)pk=2Δxyk−2Δyxk+C
其中
C=−2Δy−Δx(2b−1)(1.32)(1.32)C=−2Δy−Δx(2b−1)
在第 k+1k+1 步,決策參數可以由式(1.31)(1.31)計算得出
pk+1=2Δxyk+1−2Δy(xk+1)+C(1.33)(1.33)pk+1=2Δxyk+1−2Δy(xk+1)+C
將上述等式減去式(1.32)(1.32)可得決策值的增量δpk+1δpk+1
δpk+1=pk+1−pk=2Δx(yk+1−yk)−2Δy(1.34)(1.34)δpk+1=pk+1−pk=2Δx(yk+1−yk)−2Δy
由式(1.12)(1.12)、式(1.30)(1.30)、式(1.1)(1.1)和式(1.31)(1.31)聯立可得第一個決策值p0p0
p0=Δx−2Δy(1.35)(1.35)p0=Δx−2Δy
1.3.4 斜率小於-1
![圖1.3.4_1]()
在斜率小於-1的情況下,沿路徑像素以單位 yy 間隔取樣。假設線段以(x0,y0)(x0,y0)開始對於其路徑上已繪製的(xk,yk)(xk,yk)點我們需要判定下一個點的繪製位置是(xk+1,yk+1)(xk+1,yk+1)還是(xk,yk+1)(xk,yk+1)。
在取樣位置 yk+1yk+1 我們使用 dleftdleft 和 drightdright 來標識兩個像素位置(xkxk與xk+1xk+1)與數學位置的水平偏移量。根據式 (1.1)(1.1) 可得在像素列 yk+1yk+1 處的 xx座標計算值爲
x=(yk+1−b)m=(yk−1−b)m(1.36)(1.36)x=(yk+1−b)m=(yk−1−b)m
所以
dleft=x−xk=yk−1−bm−xk(1.37)(1.37)dleft=x−xk=yk−1−bm−xk
且
dright=xk+1−x=xk+1−yk−1−bm(1.38)(1.38)dright=xk+1−x=xk+1−yk−1−bm
爲了確定兩個像素中哪一個更接近真實路徑,需要計算兩個像素偏移的差值。
dleft−dright=2yk−1−bm−2xk−1(1.39)(1.39)dleft−dright=2yk−1−bm−2xk−1
設線段終點位置爲(x1,y1)(x1,y1),可得
m=ΔyΔx=y1−y0x1−x0(1.40)(1.40)m=ΔyΔx=y1−y0x1−x0
設決策參數 pk=Δy(dright−dleft)pk=Δy(dright−dleft)(在從左到右的繪製過程中Δy<0Δy<0 爲了保持符號統一,所以交換dleftdleft和drightdright位置)
pk=−2Δxyk+2Δyxk+C(1.41)(1.41)pk=−2Δxyk+2Δyxk+C
其中
C=2Δx(1+b)+Δy(1.42)(1.42)C=2Δx(1+b)+Δy
在第 k+1k+1 步
pk+1=−2Δx(yk−1)+2Δyxk+1+C(1.43)(1.43)pk+1=−2Δx(yk−1)+2Δyxk+1+C
將上述等式減去式(1.41)(1.41)可得決策值的增量δpk+1δpk+1
δpk+1=pk+1−pk=2Δx+2Δy(xk+1−xk)(1.44)(1.44)δpk+1=pk+1−pk=2Δx+2Δy(xk+1−xk)
目前我們有了決策值之間的增量關係,僅第一個決策值p0p0
p0=2Δx+Δy(1.45)(1.45)p0=2Δx+Δy
二、程序演示
在上面得的算法分析中,我們已經瞭解了三種算法的基本思想與設計思路。這裏通過C++程序演示其過程(也可以通過其他圖形軟件包比如Java的swing或者Android的Canvas實現),實現方式各異,不必拘泥於細節。
首先定義一個顯示用來顯示圖形的View
#ifndef lineview_h#define lienview_h#include"cxm.h"class LineView:public View{private:
_Paint _paint;//畫筆指針
_StringArray _names;//字符串數組指針
List<IntArray> *_arrays;//存放了整型數組的鏈表對象,數組中爲計算出的點的座標位置public: int bottom,top;
LineView();
~LineView(); void LineEquation(double x1,double y1,double x2,double y2);//使用直線方程畫線
void DDA(double x1,double y1,double x2,double y2);//使用DDA算法畫線
void Bresenham(double x1,double y1,double x2,double y2);//布萊森漢姆算法
virtual void onDraw(Canvas &canvas);//圖案繪製方法};
typedef LineView* _LineView;
typedef LineView& LineView_;#endif123456789101112131415161718192021接下來實現其中的構造與析構函數
LineView::LineView(){
_paint = new Paint;
_names = new StringArray(4);
_arrays = new LinkedList<IntArray>;
StringArray_ names_=*_names;
names_[0]="OpenGL";
names_[1]="Equation";
names_[2]="DDA";
names_[3]="Bresenhan";
}
LineView::~LineView(){ delete _paint; delete _names; delete _arrays;
}12345678910111213141516接下來我們實現使用直線方程的方法,該方法將計算出的點保存在了整型數組中,並將數組存儲到鏈表
void LineView::LineEquation(double x1,double y1,double x2,double y2){//y=mx+b
_IntArray _arr; double dy = y2-y1; double dx = x2-x1; double m = dy/dx; double b = y1 - m*x1; if(abs(m)>1){//以y軸像素爲單位 x=(y-b)/m
int size = abs(2*int(dy));//存放座標的數組長度
_arr = new IntArray(size);
IntArray_ arr=*_arr; int start = int(y1<y2?y1:y2);//取最小起始位置
int end = start+abs(int(dy)); for(int i=start,j=0;i<end;i++){
arr[j++]=int((i-b)/m);//x座標
arr[j++]=i;//y座標
}
}else{//以x軸像素爲單位 y=mx+b
int size = abs(2*int(dx));//存放座標的數組長度
_arr = new IntArray(size);
IntArray_ arr = *_arr; int start = int(x1<x2?x1:x2);//取最小起始位置
int end = start+abs(int(dx)); for(int i=start,j=0;i<end;i++){
arr[j++]=i;//x座標
arr[j++]=int(b+m*i);//y座標
}
}
_arrays->add(_arr);
}1234567891011121314151617181920212223242526272829然後實現使用DDA畫線的算法計算出各點
void LineView::DDA(double x1,double y1,double x2,double y2){
_IntArray _arr; double dy = y2-y1; double dx = x2-x1; double m = dy/dx; if(abs(m)>1){//以單位y取樣
double rate = 1/m; int size = abs(2*int(dy));//存放座標的數組長度
_arr = new IntArray(size);
IntArray_ arr = *_arr; int start = int(y1<y2?y1:y2);//取最小起始位置
int end = start+abs(int(dy)); double rx = y1<y2?x1:x2; for(int i=start,j=0;i<end;i++){
rx+=rate;
arr[j++]=int(rx);
arr[j++]=i;
}
}else{//以單位x取樣
double rate = m; int size = abs(2*int(dx));//存放座標的數組長度
_arr = new IntArray(size);
IntArray_ arr = *_arr; int start = int(x1<x2?x1:x2);//取最小起始位置
int end = start+abs(int(dx)); double ry = x1<x2?y1:y2; for(int i=start,j=0;i<end;i++){
ry+=rate;
arr[j++]=i;
arr[j++]=int(ry);
}
}
_arrays->add(_arr);
}12345678910111213141516171819202122232425262728293031323334最後是Bresenham算法的簡單實現
void LineView::Bresenham(double x1,double y1,double x2,double y2){
_IntArray _arr; double dy=y2-y1; double dx=x2-x1; double m = dy/dx; if(m>1){//以單位y取樣
int size = abs(2*int(dy));
_arr = new IntArray(size);
IntArray_ arr = *_arr; double p = 2*dx-dy;//po
double left = 2*dx; double right = 2*dx-2*dy; int start = int(y1); int end = start+abs(int(dy)); int x = int(x1); for(int y=start,i=0;y<=end;y++){ if(p<0){
arr[i++]=x;
p+=left;
}else{
arr[i++]=++x;
p+=right;
}
arr[i++]=y;
}
}else if(m>0&&m<1){//以單位x取樣
int size = abs(2*int(dx));
_arr = new IntArray(size);
IntArray_ arr = *_arr; double p = 2*dy-dx; double upper = 2*dy; double lower = 2*dy-2*dx; int start = int(x1); int end = start + abs(int(dx)); int y = int(y1); for(int x=start,i=0;x<=end;x++){
arr[i++]=x; if(p<0){
arr[i++]=y;
p+=upper;
}else{
arr[i++]=++y;
p+=lower;
}
}
}else if(m<0&&m>-1){//以單位x取樣
int size = abs(2*int(dx));
_arr = new IntArray(size);
IntArray_ arr = *_arr; double p = dx-2*dy; double upper = -2*dy; double lower = -2*dx-2*dy; int start = int(x1); int end = start + abs(int(dx)); int y = int(y1); for(int x=start,i=0;x<=end;x++){
arr[i++]=x; if(p<0){
arr[i++]=y;
p+=upper;
}else{
arr[i++]=--y;
p+=lower;
}
}
}else{//以單位y取樣
int size = abs(2*int(dy));
_arr = new IntArray(size);
IntArray_ arr = *_arr; double p = 2*dx+dy; double left = 2*dx; double right = 2*dx+2*dy; int start = int(y1); int end = start-abs(int(dy)); int x = int(x1); for(int y=start,i=0;y>=end;y--){ if(p<0){
arr[i++]=x;
p+=left;
}else{
arr[i++]=++x;
p+=right;
}
arr[i++]=y;
}
}
_arrays->add(_arr);
}12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788然後在onDraw方法中將所有的點繪製出來
void LineView::onDraw(Canvas &canvas){ canvas.drawLine(_paint,50,bottom,150,top); for(int i=0;i<_arrays->size();i++){ canvas.drawPoints(*_paint,*(*_arrays)[i]);
} for(int i=0;i<_names->size();i++){ canvas.drawString(*_paint,i*200+40,25,(*_names)[i]);
}
}123456789最後就是在main方法中創建視圖窗口,並將剛剛創建的View添加進去
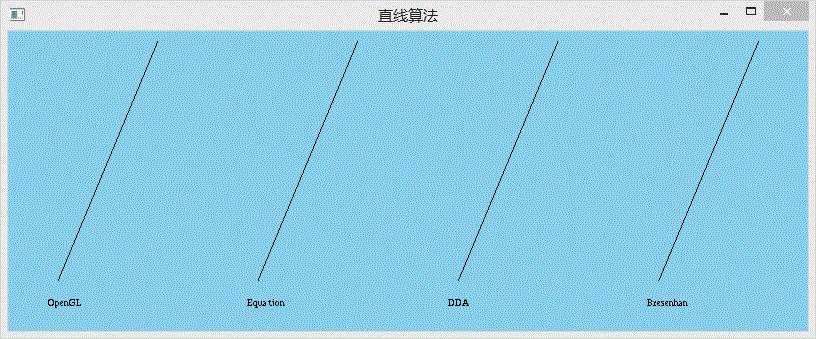
int _tmain(int argc, char* argv[]){
GlutWindow window(100,300,800,300);
String title = "直線算法";
window.setTitle(title);
window.setBackgroundColor(BLUE_SKY);
_LineView _view = new LineView();
LineView_ view=*_view;
view.bottom=50;
view.top=290;
view.LineEquation(250,view.bottom,350,view.top);
view.DDA(450,view.bottom,550,view.top);
view.Bresenham(650,view.bottom,750,view.top);
window.addView(view);
window.show(&argc,argv);
return 0;}1234567891011121314151617181920結果圖展示
![圖2_1]()
Donald Hearn.計算機圖形學 第四版.電子工業出版社.2016-2.2th.101~107