一、均數與標準差
【例1】本組105 例, 男55例, 女50例; 平均年齡:62.3±6.1歲,所有入選病例均符合1999年WHO高血壓診斷標準。
舉這個例子是爲了說明“均數”與“標準差”的概念。我實在不願意多花時間闡述一些概念性的東西,但是由於“標準差”實在太重要了。【例1】中的 數據“62.3±6.1”,“62.3”就是年齡的均數,均數的概念大家都懂,那麼後面的“6.1”是什麼呢?它就是標準差。有人可能會問,表達一組人的 平均年齡,用均數就夠了,爲什麼還要加一個標準差呢?先看下面的一個例子:有兩組人,第1組身高(cm):98、99、100、101、102;第2組身 高(cm):80、90、100、110、120,這兩組人雖然身高的均數都是100cm,但是,仔細觀察,第1組的身高很接近,第2組的身高差別很大, 故僅僅用一個平均數表達一組數據的特徵是不完整的,還需要用另一個指標來表達其參差不齊的程度,這就是標準差。統計學上對一組測量結果的數據都要用“均 數±標準差”表示,習慣表達代號是:,具體例子如:平均收縮壓120±10.2mmHg。
我想現在大家都已知道標準差是什麼東東了,那麼,標準差是怎樣得到的呢?有一個比較複雜的計算公式,我們不必去深究這個公式是怎麼樣的,只需知道標準差越小,說明數據越集中,標準差越大,說明數據越分散。
撰寫醫學論文的第一步是收集原始數據,如:
第1組身高(cm):98、99、100、101、102;
第2組身高(cm):80、90、100、110、120。
在論文中並不是直接給出原始數據,而是要以方式表示。利用軟件《臨牀醫師統計學助手 V3.0》,只要輸入原始數據,就能自動計算出均數及標準差,即第1組平均身高:100±1.58cm;第2組平均身高:100±15.81cm,如下圖。
二、兩樣本均數差別T檢驗
【例2】目的 研究中藥板蘭根對“非典”療效。方法 將36例“非典”患者隨機分爲治療組19例,採用常規治療+板蘭根口服,對照組17例,僅採用常規治療。結果 治療組平均退熱時間3.28±1.51d;對照組平均退熱時間5.65±1.96d,兩組間對照差別有極顯著意義(p<0.01
這是最常見的一種統計學數據處理類型,統計學述語叫做“兩樣本均數差別T檢驗”,說得通俗易懂一些,就是檢驗兩組方法所得到的數據到底有沒有差異,或者說,差異是否有意義。我們平時的思維習慣是,數據的大小還用得着檢驗嗎?這是小學生都會的問題。可是別忘記了現在是在搞科研,科學方法看問題可不一定這麼簡單。
可能還沒有說明白這個問題,下面舉一個簡單的例子。我們的目的是得出這樣一個結論:“北京出產的西瓜比上海出產的西瓜大”。最可靠的方法是把所有北京的西 瓜和上海的西瓜都測量重量,得到兩個均數,然後比大小即可,可是智商正常的人並不會這樣去做,通常的做法是,隨機選一部分北京的西瓜和一部分上海的西瓜, 先讓這兩部分西瓜比大小,然後推斷到底那裏的西瓜大。這種方法是“窺一斑可見全豹”,統計學述語叫做“由樣本推斷總體”,事實上,我們所做的醫學科研都是 基於這種方法。
再回到上面的例子,假如我們有二種做法:
A、隨機選2個北京西瓜,平均重量是5.6±0.3kg;再隨機選2個上海西瓜,平均重量是4.3±0.25kg;
B、隨機選1000個北京西瓜,平均重量是5.6±0.3kg;再隨機選1000個上海西瓜,平均重量是4.3±0.25kg。
憑生活常識,由B推出“北京的西瓜比上海西瓜大”這個結論的把握性就非常的大,而A則基本上推不出這個結論。現在,終於可以引出我們的主題了,統計學處理本 質是考查由樣本差異推斷總體差異的把握性有多大,這種把握性在統計學上由P值表示。如P<0.05或P<0.01,可以理解爲由樣本差異推斷總體差異的把 握性達95%或99%以上,兩組數據差異有顯著意義;如P>0.05,可以理解爲這種把握性在95%以下,兩組數據差異沒有顯著意義。
上面所講的實已爲統計學之精髓,建議多看幾遍,如果天生愚魯,還是看不太懂,也沒有關係,現在進一步“傻瓜化”,即所謂統計學處理,只要求得P值即可。P<0.05或P<0.01,表示陽性結果,兩組數據差異有顯著意義;P>0.05,表示陰性結果,兩組數據差異沒有顯著意義。所以,統計學處理的中心任務是求P值。
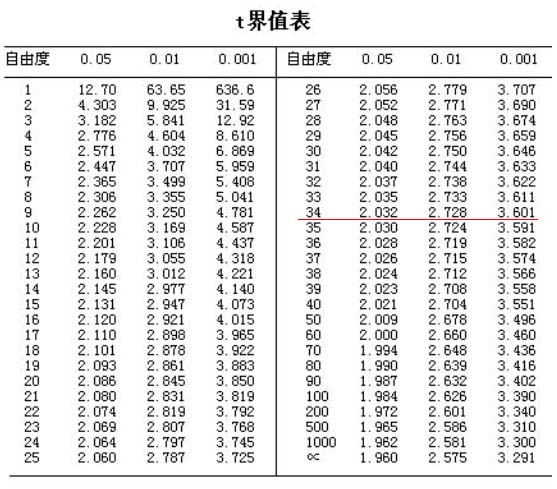
下面講解遇到【例2】這樣的問題,如何求P值。【例 2】中一共有6個數據:第一組均數(X1)、標準差(S1)、例數(N1)與第二組均數(X2)、標準差(S2)、例數(N2),就是根據這6個數據,先 通過複雜計算,求出“T”值(如果沒有想成爲統計學專家,就不必去理解“T”是什麼了,知道“T”是爲了求“P”用的就可以了),求出“T”值後,再查 “T界值表”,就知道“P值”了。
具體解法步驟如下:
⑴ 通過計算(這裏略去計算公式,可由軟件求出),T=4.088
⑵ 計算自由度:自由度=N1+N2-2=19+17-2=34(計算自由度是爲了查T界值表用的,自由度即兩組例數之和減去2,不要問我爲什麼不減去3或減去1這樣的問題了。)
⑶ 查T界值表,對應自由度34,T0.05=2.032,T0.01=2.728,今T=4.088>T0.01,即P<0.01,差別有高度顯著意義。
T=4.088是如何求出的呢?我們再回到軟件《臨牀醫師統計學助手 V3.0》,只要把第一組均數(X1)、標準差(S1)、例數(N1)與第二組均數(X2)、標準差(S2)、例數(N2)這6個數據輸入對應的框內,該軟件就會利用預先存儲的公式自動計算T值,並查T界值表,得到P值,如圖:
三、配對計量資料T檢驗
【例3】目的 研究音樂胎教對胎兒運動技能培養的效果。方法 10例28~32周孕婦,分別記錄聽音樂(水滸傳主題曲)前每小時的胎動次數及聽音樂後每小時的胎動次數,結果 數據如表1所示,音樂胎教後胎動次數增多,差別有顯著意義(p<0.05 )結論 音樂胎教可增強胎兒運動技能,對培養我國運動天才有現實意義。
顯然【例3】與【例2】有所不同,主要是【例3】兩組間的數據可以前後配對的。我們經常碰到這種情況,即同一個體做兩次處理,如治療前檢測某一指標,治療 後再檢測某一指標,而後做治療前後配對比較,以判斷療效,正如【例3】。這種情況如何進行統計學處理呢?同樣也是先計算T值,然後按自由度(這時自由度= 對子數-1,如本例自由度是9。)查T界值表,求得P值。
但是“配對T檢驗”計算T值的方法與“兩樣本均數T檢驗”有所不同,這裏不再作介紹,由軟件《臨牀醫師統計學助手 V3.0》自動完成即可,如下圖。本例T=2.47,自由度=10-1=9,查T界值表,對應自由度9,T0.05=2.26,T0.01=3.25,今T=2.47>T0.05,即P<0.05,差別有顯著意義。
可能有人會問,【例3】的情況,也可以把胎教前視爲對照組,求得平均胎動次數是:21.8±5.31,胎教後視爲治療組,求得平均胎動次數是:24.0±6.31,然後套用【例2】的方法,用“兩樣本均數T檢驗”行不行?這樣雖無大錯誤,但是將會導致檢驗效率的下降,就是說,如果數據差異較大時,兩種方法均可,如果數據差異較小時,用“配對T檢驗”會顯示出差異有意義,而用“兩樣本均數T檢驗”時,可能差異無意義。切記,非配對資料誤用配對T檢驗,則是錯誤的。
四、計數資料卡方檢驗
【例4】目的 研究醫患關係對重症病人死亡率的影響。方法 根據問卷調查對收住重症監護病房的病人分爲“醫患關係良好組”與“醫患關係緊張組”,比較兩組間的住院死亡率。結果 “醫患關係良好組”25例,住院間死亡3例,死亡率13.6%,“醫患關係緊張組”23例,住院間死亡9例,死亡率39.1%,兩組間差別有顯著意義(p<0.05 )結論 醫患關係緊張增加重症病人的住院死亡率,可能與醫師害怕被病人告而治療方案趨向保守有關。
【例4】又是一個非常常見的一種統計學數據處理類型。【例4】中所提供的數據是“比例”,或百分數,與前面三個例子不同,前面三個例子所提供的數據則是直接在病人身上測量到的數據,如收縮壓120±10.2mmHg、身高100±15.81cm等,我們把【例4】中的數據叫做計數資料,而【例1、2、3】中的數據叫做計量資料。計數資料無法用形式表示,只能用比例表示,如:死亡率13.6%、30例中顯效10例(10/30)等。
顯然,對於計數資料,再用T檢是不適合了,必須用卡方檢驗。卡方檢驗的步驟是:先求出X2(類似於T檢驗時先求T值)值,然後進行判斷:
⑴ 如果X2<3.84,則P>0.05;
⑵ 如果X2>3.84,則P<0.05;
⑶ 如果X2>6.63,則P<0.01。
解釋一下,上面的兩個數字“3.84”與“6.63”是查“X2界值表”得來的,只要記住即可。
所以,卡方檢驗的關鍵是求出X2值。爲了求出X2值,必須先介紹“四表格”概念。“四表格”的形式如下,關鍵數據是 a、b、c、d 四個數,X2值就是通過這四個數據計算出來的(這裏仍不介紹公式,由軟件計算。)。
現將【例4】中的數據填入“四表格”即如下圖。
當你學會了填“四表格”數據之後,就能利用軟件《臨牀醫師統計學助手 V3.0》非常容易的進行卡方檢驗了,本軟件提供與“四表格”完全相同的界面,把數據填寫正確之後,就自動計算X2值並判斷結果,【例4】X2=4.702>3.84,故P<0.05,如下圖:
在此說明一下,大家可能已注意到本軟件中出現的“理論數(T)”,在此不解釋“理論數(T)”是什麼,只要記住,當例數(n)<40或T<1時,應採用“精確概率法”,這個方法太複雜,在此不作介紹。
現在已經講完了4個實例,掌握本教程的訣竅是將實際中碰的的情況,對照實例,“對號入座”即可,而具體計算過程,可由軟件去完成。